문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
예제 입력 1
3
예제 출력 1
7
1 3
1 2
3 2
1 3
2 1
2 3
1 3찾아보니까 재귀 문제 중에서는 가장 유명한 문제 중 하나인 것 같다. 원판 각각을 생각하면 말도 안되게 복잡한 문제처럼 보이는 데, 재귀를 사용하면 정말 간단하게 해석가능한 문제라고 평가할 수 있겠다.
해법의 아이디어는 간단하다. 쌓인 원판들을 각각 생각하지 말고, 밑의 가장 큰 원판 하나와 위에 쌓인 나머지 원판의 묶음 하나, 즉 2 개의 원판이 쌓여 있다 가정하는 것이다. 다음 그림과 같이 말이다.
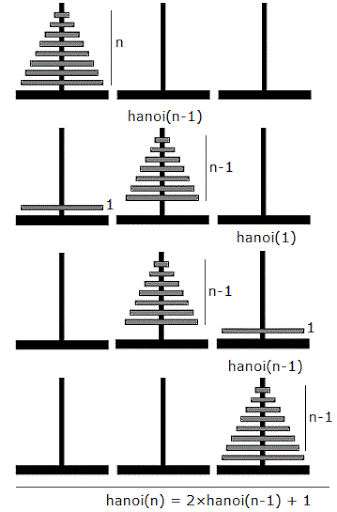
원판이 2 개만 있는 경우 문제는 간단해진다. 순서는 다음과 같다.
- 가장 작은 원판을 버퍼가 되는 축에 끼운다.
- 가장 큰 원판을 도착 축에 끼운다.
- 버퍼 축에 끼워진 원판을 도착 축에 끼운다.
코드는 다음과 같다.
#include <iostream>
void hanoi(int N, int start, int end, int buffer) {
if (N==1) {
std::cout << start << " " << end <<"\n";
}
else {
hanoi(N - 1, start, buffer, end);
std::cout << start << " " << end <<"\n";
hanoi(N - 1, buffer, end, start);
}
}
int main() {
int N;
std::cin >> N;
std::cout << (1<<N)-1 <<"\n";
hanoi(N, 1, 3, 2);
return 0;
}묶어서 보는 아이디어를 떠올리는 데 오래걸렸던 문제이다. 마지막에 답은 잘 나오는 데 시간 초과가 떠서 애를 먹기도 했다. 남들이 짠 코드를 보았는데 특별하게 시간을 잡아먹는 부분도 없었는데 말이다. 결과적으로 std::endl을 그냥 "\n"으로 바꾸니까 해결이 되었다. std::endl 대신 "\n"을 사용하는 것 소소한 팁이라면 팁일 수 있겠다. 이 것으로 글을 마친다.
'컴퓨터 과학 > 자료구조 및 알고리즘' 카테고리의 다른 글
| GCD 알고리즘 (1) | 2023.11.25 |
|---|---|
| 백준 2798, 블랙잭 (0) | 2022.11.21 |
| 백준 2447, 별 찍기-10 (0) | 2022.10.20 |
| 백준 10870, 피보나치 5 (1) | 2022.10.19 |
| 백준 2749, 피보나치 수 3 (2) | 2022.09.21 |



